This article explains in detail what genetic algorithms are and what role they play in machine learning.
We will focus on genetic algorithms, which appeared much earlier than neural networks, but have now been adopted GA by NN. Although GA still has real life applications such as optimization problems like scheduling, games, robotics, hardware design, commutative problems, etc.
Genetic algorithms are algorithms based on the evolutionary idea of natural selection and genetics. GA are adaptive heuristic search algorithms, meaning that the algorithms follow an iterative pattern that changes over time. It is a type of reinforcement learning where feedback is required without indicating the correct path. The feedback can be positive or negative.
Why use genetic algorithms?
GA are more reliable algorithms that can be used for various optimization problems. Unlike other artificial intelligence algorithms, these algorithms do not deviate easily in the presence of noise. GA can be used to search a large space or multimodal space.
Biological background of genetic algorithms
Genetics is derived from the Greek word 'genesis', which means to grow. Genetics determines the factors of heredity, similarities and differences between offspring in the process of evolution. Genetic algorithms also derive from natural evolution.
Some terminology from biology
- Chromosomes: All the genetic information of a species is stored in chromosomes.
- Genes: Chromosomes are divided into several parts called genes.
- Alleles: Genes determine the characteristics of an individual. The ability of genes to combine to form characteristics is called alleles. A gene can have different alleles.
- Gene pool: All possible combinations of genes that are alleles in a population pool are called a gene pool.
- Genome: The set of genes of a species is called the genome.
- Position: Each gene has a position in the genome called a locus.
- Genotype: The complete combination of genes of an individual is called the genotype.
- Phenotype: The collection of genotypes in decoded form is called the phenotype.
What are genetic algorithms?
Genetic algorithms drive the evolutionary process, as in natural systems. Charles Darwin established the theory of evolution, according to which biological beings evolve in natural evolution according to the principle of "survival of the fittest." The search on AH aims to promote the "survival of the fittest" theory.
GAs perform random searches to solve optimization problems. GA uses techniques that leverage prior historical information to direct its search toward optimization in a new search space.
Correlation of chromosomes with GAs.
The human body has chromosomes, which consist of genes. The set of all genes of a particular species is called a genome. In living organisms, genomes are stored in different chromosomes, while in GA all genes are stored on the same chromosome.
Comparison between natural genetics and the terminology of genetic algorithms:
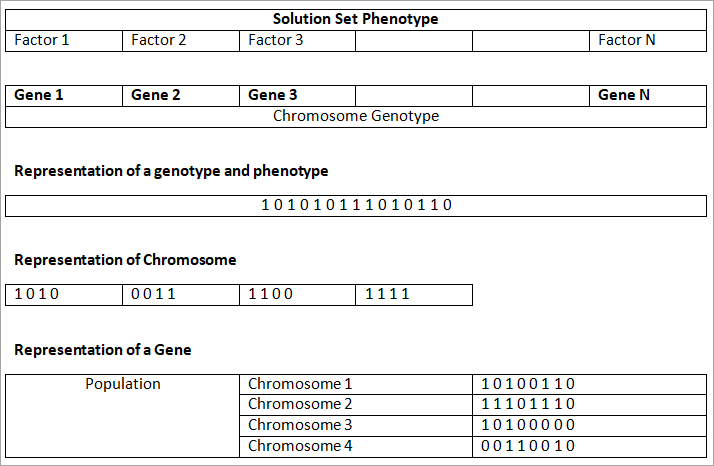
Important terminology in GA
- Population: it is a group of individuals. The population includes the number of individuals studied, information about the search space, and phenotype parameters. In general, the population is initialised randomly.
- Individuals: individuals are a single solution in a population. An individual has a set of parameters called genes. Genes are combined to form chromosomes.
- Genes: Genes are the building blocks of genetic algorithms. A chromosome is composed of genes. Genes can determine the solution to a problem. They are represented by a sequence of bits (0 or 1) of arbitrary length.
- Fitness: The fitness indicates the value of the phenotype of the problem. The fitness function indicates how close the solution is to the optimal solution. The fitness function is determined in various ways, e.g., by the sum of all parameters associated with the problem - Euclidean distance, etc. There is no rule for evaluating the fitness function.
Simple GA presentation:
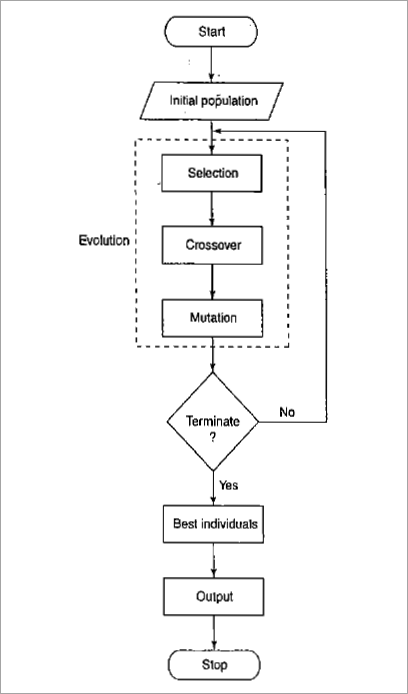
A simple genetic algorithm looks like this:
- Start with a randomly generated population.
- Calculate the fitness function of each chromosome.
- Repeat the steps until n offspring are generated.
The offspring are generated as shown below.
- Select a pair of chromosomes from the population.
- Cross the pair with probability to generate offspring.
- Mutate the cross with probability .
- Replace the original population with the new population and go to step
Let us see the steps to follow in this iteration process.
Initial population of chromosomes is created. The initial population should contain enough genes to generate any solution. The initial population pool is generated randomly.
Selection: The best set of genes is selected based on the fitness function. The string with the best fitness function is selected.
Reproduction: new offspring are generated by recombination and mutation.
Evaluation: The newly generated chromosomes are evaluated for fitness.
Replacement: In this stage, the old population is replaced by the newly generated population.
Selection methods:
Roulette selection: In this method, a linear search is performed using a roulette wheel. The slots in the wheel are weighted according to the individual fitness value. The target value is randomly determined according to the proportion of the sum of the fitnesses in the population.
The population is then searched until the target value is reached. This method does not guarantee the strongest of individuals, but has a probability of being the strongest.
Rank selection: In this method, each chromosome is assigned a match value from the rank. The worst fitness is 1 and the best fitness is N. This is a slow convergence method. In this method, diversity is maintained which leads to a successful search.
Potential parents are selected and then a tournament is held to decide which person becomes the parent.
Tournament selection: In this method, a selective pressure strategy is applied on the population. The best person is the one with the highest fitness. This individual is the winner of the tournament competition among Nu individuals in the population.
The tournament population including the winner is added back to the pool to generate new offspring. The difference in fitness between the winner and the individuals in the mating pool provides selective pressure for optimal performance.
Crossover
This is the process of creating a baby from 2 individuals.
The process of breeding after selection produces clones with good pricks. The crossover operator is applied to strings to produce better offspring.
The implementation of the crossover operator is as follows:
Two individuals are randomly selected from the population to produce offspring.
The crossover point is randomly selected along the length of the string. The values at this point are interchanged.
Crossing can be performed as one-point, two-point, multiple-point, and so on. In a one-point crossing there is one crossing point, while in a two-point crossing there are two points where values are swapped.
This can be seen in the following example:
One-point intersection

Mutation
Mutation follows crossover. While Crossover focuses only on the current solution, Mutation searches the entire search space. This method is about recovering lost genetic information and spreading genetic information.
This operator helps to maintain the genetic diversity of the population. It helps to avoid local minima and prevents the generation of useless solutions from a population.
Mutation can be performed in several ways, such as reversing the value of each gene with low probability or performing mutation only if it improves the quality of the solution.
When to stop a genetic algorithm?
The genetic algorithm is stopped when the following conditions are met:
1) Best individual convergence: when the minimum fitness level falls below the convergence value, the algorithm is stopped. This leads to a faster convergence.
2) Worst individual convergence: when the least fit individuals in the population reach a minimum fitness level below the convergence, the algorithm is stopped. In this method, the minimum fitness standard in the population is maintained. This means that the best individual is not guaranteed, but individuals with minimum fitness will be present.
3) Sum of fitness: In this method, if the sum of fitness is less than or equal to the convergence value, the search is stopped. It guarantees that the entire population is within the fitness range.
4) Median fitness: In this method, at least half of the individuals in the population are better than or equal to the convergence value.
A convergence criterion or stopping condition can be:
- When a certain number of generations have evolved.
- After a certain period of time in which the algorithm is executed.
- When the population fit value does not change further with the iterations.
Conclusion
Genetic algorithms are based on the method of natural evolution. These algorithms differ from other classification algorithms because they use coded parameters (0 or 1), there are many numbers of individuals in the population and they use a probabilistic convergence method.
With the process of crossover and mutation, GAs converge in successive generations. Performing a GA algorithm does not always guarantee a successful solution. Genetic algorithms are very efficient in optimization - task scheduling problems.